Review: The joy of symmetry
- 29 July 2006
- From New Scientist Print Edition
- Justin Mullins
Book Details:
- The Equation that Couldn’t be Solved
- by Mario Livio
- Simon & Schuster/Souvenir Press
- $26.95/£20
- ISBN 0743258207/0285637436
Book Details:
- Fearless Symmetry
- by Avner Ash and Robert Gross
- Princeton University Press
- $24.95/£15.95
- ISBN 0691124922
WHAT keeps you turning the pages of a book long into the early hours of the morning? The Da Vinci Code, for example, grips you with an unexplained death and a secret the church has hidden for two millennia. How can a book about mathematics compete?
What the authors promise in The Equation that Couldn’t be Solved and Fearless Symmetry is mathematical beauty – to be more precise, a tour of the beautiful but mysterious world of symmetry. Stick with us, they say, and for a few hours of your time, we will show you a hidden world of unadulterated mathematical magnificence.
One of the greatest secrets of mathematics is its hidden beauty. It doesn’t reveal itself to every mathematical traveller, though. As students, most of us take a dreary tour of basic arithmetic and calculus. That is a bit like going around Vatican City without getting off the bus. You will get a glimpse of St Peter’s Basilica but you’ll miss the Gallery of Maps, Da Vinci’s portrait of Saint Jerome and the Sistine Chapel.
If you want to see these, you are better off hiring a guide to tell you their story and explain their hidden meanings. That’s the role astrophysicist Mario Livio takes in The Equation that Couldn’t be Solved. Livio’s book is largely about the world of algebra and how it was discovered. It is a neighbourhood that you would have passed through briefly in your youth, so you might be familiar with the quadratic equation ax2 + bx + c = 0. With a bit of mathematical sleight of hand it is possible to show that the solution is:
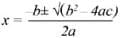
What about equations of the form ax3 + bx2 + cx + d = 0? Can these “cubic” equations be solved in the same way? Yes, as can quartics where the largest term is ax4. But something strange happens with quintics, in which the largest term is raised to the power of 5. Mathematicians puzzled over quintics for centuries, until a young Frenchman called Évariste Galois discovered how symmetry unlocks the door to this mathematical landscape. Galois was never able to build on his discovery as, in a story that Dan Brown would be proud of, he died at the age of 21 in a duel over a woman who had spurned his advances.
Livio is a knowledgeable guide who reveals a part of the mathematical world of symmetry that most people would be unlikely to find on their own. When he reaches the domain of professional mathematicians, Livio relies on his skills as a storyteller to describe the parts of the landscape that are beyond our reach. Still, unless you have travelled there yourself, you will never really know what it is like.
In Fearless Symmetry, Avner Ash and Robert Gross make one of the bravest attempts yet to guide the mathematical novitiate up the highest mountains in the world of symmetry. Ash and Gross are not satisfied with merely telling us what it is like at the summit, they actually attempt to take us there, a task akin to taking day-trippers up Everest.
They guide us skilfully through the foothills – in the form of group theory, the language of symmetry – but most of the book is an attempt on the summit. Here they show how to use symmetry to study equations such as the quintic. From the summit, Ash and Gross even point out the frontiers of the land that mathematicians are struggling to explore today.
By its nature, the ground is hard, and even with Ash and Gross’s light-hearted help and thoughtful shortcuts, it is easy to lose your way. The truth is that many readers may not make it to the summit on their first attempt. That doesn’t matter. The view from the top is spectacular but from halfway up, it’s pretty good too.
Justin Mullins’s mathematical photography is part of the 2006 Bridges Exhibit of Mathematical Art at the Institute of Education in London, 4–9 August
From issue 2562 of New Scientist magazine, 29 July 2006, page 48